複利の効果とは　長期投資はなぜ資産形成に有利といわれるの？

「銀行にお金を預けても、なかなか増えない」と感じていらっしゃる方も多いのではないでしょうか。
低金利と物価上昇が続く現在、預貯金だけでは大切な資産が目減りしてしまうリスクがあります。

そこで鍵となるのが、お金がお金を生む「複利」の力と、それを最大限に活かす「長期投資」です。
本コラムでは、複利の基本的な仕組みを分かりやすく解説し、インフレ時代に長期投資がいかに有効か、その意義を掘り下げていきます。

複利とは利子にもまた利子がつくこと

利子にもまた利子がつくことを、「複利」といいます。^*1
では、複利の計算方法はどのようなもので、単利との違いはどこにあるのでしょうか。

複利の計算方法

元金（もともとのお金）が100万円あり、この100万円を金利5％（年利）で1年間預金したとしましょう。
すると、1年後の元利合計（元本と利息を合わせた金額）は、元本100万円と利息5万円を足した、105万円になります。
この場合、5万円は、元金に対してついた利子です。

この5万円も含めた105万円を再び金利5％で1年間預けると、1年後には110万2,500円となります。

1年後　100万円（元本） × 1.05（年利） = 105万円（元利合計）
2年後（複利）　105万円 （元本）× 1.05（年利） = 110万2,500円（元利合計）

2年後の2,500円は、利子である5万円についた利子です。
これが複利効果です。

同様に、元本100万円を、年利率5%で10年間複利運用した場合はどのくらいの利子がつくのでしょうか。

10年後の元利合計 = 100万円 × (1 + 0.05) 10 = 100万円 × 1.62889 ≒ 162.89万円
となり、利子は約63万円にまで増えることになります。

※当該期間中の金利を一定と仮定して複利運用した場合の概算値です。税金等を考慮していません。

単利との違い

一方、利子を元金に組み入れない場合は「単利」となります。
上記の例で、利子5万円を元金100万円に組み入れず、100万円のみを再び金利5％で預けたとすると、その1年後には110万円になります。

1年後　　　　100万円（元本） × 1.05（年利） = 105万円（元利合計）
2年後（単利）100万円 + 5万円（1年目の利子）+ 5万円（2年目の利子）= 110万円（元利合計）

100万円を年利5％で40年運用するとどうなるでしょうか（図1）。^*2

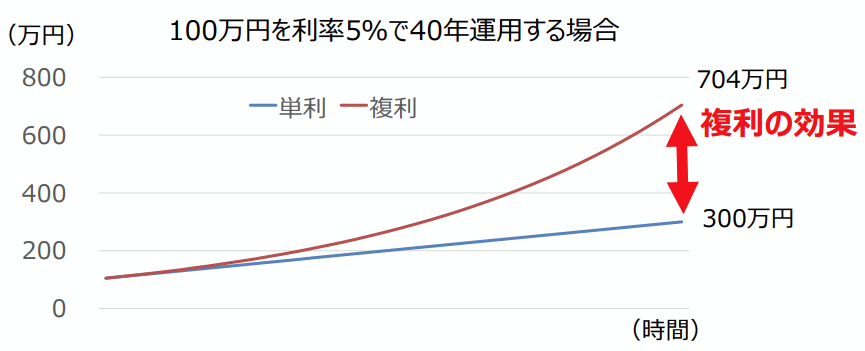
図1　【100万円を年利5%で40年運用する場合の単利と複利効果】
出所）金融庁「高校生のための金融リテラシー講座」p.62

40年間、運用した場合は、単利と複利の差は404万円にも上ります。

※上記はシミュレーションの際に設定した条件であり、実際の運用成果とは異なります。また、税金・手数料等を考慮しておりません。
※預貯金以外の運用性金融商品にはリスクが伴います。したがって、元本保証もありません。

複利効果を生かした長期投資が必要なのはなぜ？

現在は、こうした複利効果を活かした長期投資が必要です。
それはなぜでしょうか。

低金利時代

現在は低金利のため、銀行にお金を預けても、なかなか増えないという問題があります。

日本銀行によると、2025年7月の預金種類別の店頭表示金利は、普通預金が年利0.183％、定期預金に1千万円以上、1年預けた場合の年利は0.256％となっています。^*3

ここで、「72の法則」によって、金利を実感してみましょう。^*2
「72の法則」とは、元本が2倍になる金利と年数の関係を表したものです（図2）。

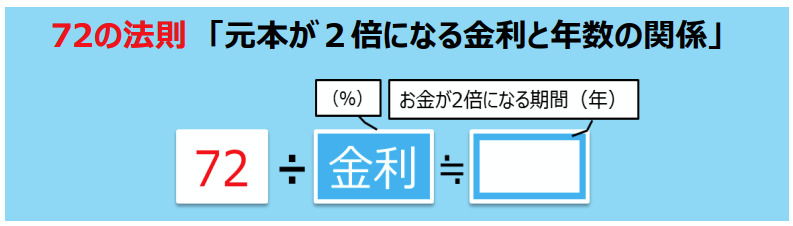
図2　【72の法則】
出所）「高校生のための金融リテラシー講座」p.63

これにさまざまな金利を当てはめてみましょう。
もし、金利が8％なら、72 ÷ 8 = 9 で、元本が2倍になるのにかかる期間は9年になります。
次に、金利が6％だったら、72 ÷ 6 = 12 で、元本が2倍になるまで12年かかります。

では、現在の金利だとどうなるでしょうか。現在の金利を0.2％として計算すると　
　　　72 ÷ 0.2 = 360 となります。
現在の金利では、元本が倍になるまで、なんと約360年もかかってしまうのです。

※ 資産を2倍にふやすために必要な運用年数は、当該期間中の金利を一定と仮定して複利運用した場合の概算値です。また、税金等を考慮していません。

物価の上昇

「お金」の価値と、物価（物やサービスの価格）は、表裏一体の関係です。^*4
物価が下がっている状態をデフレ、上がっている状態をインフレと呼びます。
「物価が下がっていること（デフレ）は、お金の価値（物やサービスを買う力 = 購買力）が上がっていること」、「物価が上がっていること（インフレ）は、お金の価値が下がっていること」といい換えることができます。
では、現在はどうでしょうか。以下の図3は消費者物価指数の推移を表しています。^*5

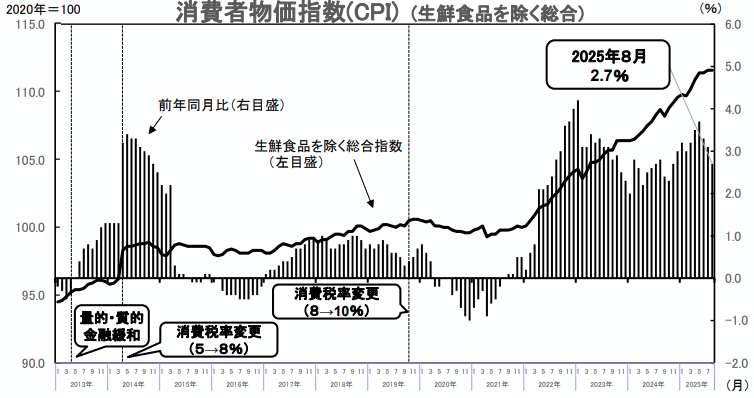
図3　【消費者物価指数】
出所）総務省「消費者物価指数（全国8月）」p.2

現在は、物価が上昇傾向です。
2020年を100とした物価指数は上昇を続け、2025年8月の「生鮮食品を除く総合」の物価は、前年同月比 2.7％でした。

このように、金利は低く、物価が上昇傾向であるインフレの現在は、預貯金だけではお金の価値が下がってしまうという状況があるのです。

長期投資には複利効果を活かせるメリットがある

次に、長期投資のメリットを考えていきましょう。

複利効果が活かせる

利息が利息を呼ぶ複利の効果は、期間が長いほど効果が大きくなることが期待できます。^*6

ここで、NISAのつみたて投資枠で、長期投資する際のシミュレーションをみてみましょう。
NISAは、家計の安定的な資産形成を支援するための制度です。^*7

NISA口座で投資した一定の購入分は、通常、課税対象となる株式や投資信託などから得られた配当や分配金、売却時の譲渡益が非課税になります。

※上記はNISAの概要をお知らせするための簡易的な説明であり、全ての情報を網羅したものではありません。今後の法令・制度の変更等により、内容は変更となる可能性があることにご留意ください。
※上記の説明は制度に基づく一般的なものであり、金融機関ごとに異なる対応となる場合があります。

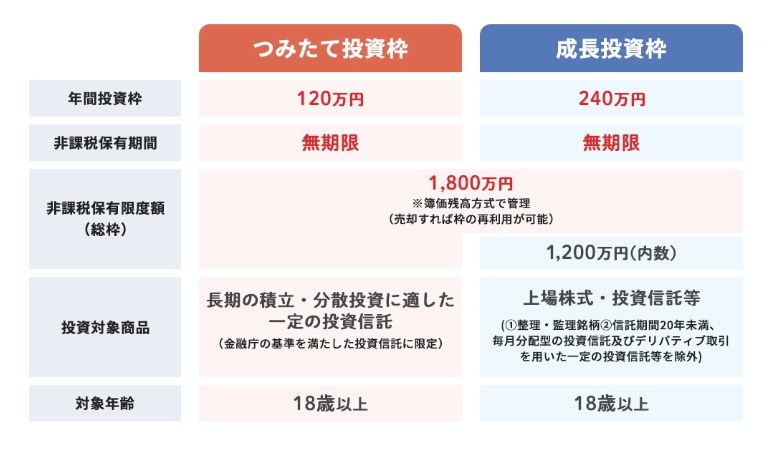
図4　【NISAの概要】
出所）政府広報オンライン「『NISA』って何？わかりやすく解説」（2024年9月30日）

年間投資枠は、「つみたて投資枠」が120万円、「成長投資枠」が240万円で、非課税の保有限度額（総枠）は1,800万円です。

長期の投資プランとして、30年かけて非課税投資枠を使い切る場合は、月々5万円、年間60万円を投資することになります。^*8
利回りを5%と想定し、複利運用した場合、30年後には元本の1,800万円はいくらまで増えるのでしょうか（図5）。

図5　【毎月5万円ずつ利回り5％で複利運用した場合の投資元本と運用利益】
出所）三菱ＵＦＪモルガン・スタンレー証券「NISAの投資シミュレーション！1,800万円は5・10・20・30年後いくらになる？」（2025年3月21日）

30年目には投資元本1,800万円に対して、元本を超える約2,361万円の運用益が得られ、資産総額は約4,161万円に達する計算です。
これが、長期投資による複利効果です。

※上記はシミュレーションの際に設定した条件であり、実際の運用成果とは異なります。また、税金・手数料等を考慮しておりません。
※預貯金以外の運用性金融商品にはリスクが伴います。したがって、元本保証もありません。

長期投資には他にもメリットがある

長期投資には、他にもさまざまなメリットがあります。^*6

●収益率が安定する傾向がある
投資期間を長くすることで、運用成績の悪い時期と良い時期がならされ、平均的な収益率が安定する傾向があります。

●長期的な視点で投資に取り組める
短期的な見方や時々のトレンドに惑わされることなく、長期的な視点で投資に取り組めます。

●失敗しにくい投資の仕組みを活用できる
心理的バイアスを排除するために積立ルールを作り、リスクを減らす目的で分散投資を行えば、長期投資のメリットを活かすことができると期待されます。

分散投資とは、1つの資産だけでなく、値動きの異なる複数の資産に投資を行うことです。また、投資先の地域を分散することで、より安定的に利益を得ることが期待でき、リスクを軽減することが期待できます。

※長期投資や分散投資は将来の収益や相場下落時の損失回避を保証するものではありません。

おわりに

低金利とインフレが続く今は、預貯金だけでは実質的な資産価値が目減りするリスクがあります。
しかし、時間を味方につける「複利」の力を活用すれば、着実に資産形成を進めることが期待できます。

NISAのような制度を利用し、少額からでも長期投資を実践することが、将来の豊かな生活を実現する鍵となると思われます。